Today we're going to discuss what an IP address actually is. Additionally, we'll discuss subnet masks along with the CIDR notation.
ASSESSMENT: An assessment containing exercises is provided at the end of the article to aid your comprehension. It is highly encouraged to complete the assessment to verify your understanding of the material.
Topics discussed
- Binary
- Bitwise operations
- IP addresses
- Subnet masks
- CIDR (Classless Inter-Domain Routing)
Binary
Watch this 5 minute YouTube video for a quick lesson on the binary number system. A basic understanding of the binary number system is important since computers internally represent IP addresses in binary.
Bitwise operations
For this article, the only bitwise operations we need to be familiar with are bitwise AND and the left shift.
Bitwise AND
In boolean logic, the expression P AND Q is true only when P is true and Q is true. The truth table for AND looks like so:

Now instead of True and False values, we're dealing with bits which have a value of 0 or 1. With bits, 0 is treated as False while 1 is treated as True. The symbol for bitwise AND is a single ampersand (&)

Let's look at some bitwise AND examples. According to python,
>>> 12 & 9 8
How did 12 & 9 evaluate to 8? Let's convert both 12 and 9 to binary and then
line up their binary bits.

Now, we pair up the bits by column. We pair the first bit of 12 with the first bit of 9, the second bit of 12 with the second bit of 9, and so on. For each pair, we perform a bitwise AND

So the first bit of 12 & 9 will be 1 & 1, the second bit of 12 & 9 will be
1 & 0, and so on. Then we use the truth table for bitwise AND to figure out
the value of each bitwise AND expression between the pairs. Then we can convert
the resulting binary value to decimal.

As another example, let's determine the result of 13 & 7. We'll use the same
process as before.
First, we convert each number to binary and then line up their bits. Since 13 requires 4 bits and 7 only requires 3 bits, we will pad 7 with a leading 0 so both numbers will use the same number of bits.

Then we pair up the bits of the two numbers by column, and we bitwise AND each column.

Then we use the truth table to evaluate the bitwise AND of each pair, and then we convert our result to decimal.

Our answer appears to be 5. Is this correct? According to Python...
>>> 13 & 7 5
Left shifts
Given an integer, it's possible to "shift" the bits of the integer over. The
notation a << n means "shift the bits of the integer a over to the left n
times". We will demonstrate how left-shifts operate.
Suppose we have a 4-bit integer x assigned to 13. Note that
$$13_{10} = 1101_{2}$$

Suppose we wanted to shift the bits of x over to the left by 1. According to
the notation presented above, if we want to "shift the bits of the integer x
over to the left 1 times", we denote this with x << 1. To perform this
shift, we just scoot all the bits over to the left by 1.

Bits that were moved beyond the left boundary are discarded. The blank spaces introduced on the right are filled with 0's.

So for a 4-bit integer x assigned 13, x << 1 equals $10$.
Does the size of the integer being shifted matter? In other words, does it
matter if x is a 4-bit, 8-bit, or 16-bit integer? Let's see. Suppose we have a
8-bit integer x assigned to 13.

Let's perform the same operation, x << 1. So we shift each bit in the
sequence over to the left once.

Bits that were moved beyond the left boundary are discarded. The blank spaces introduced on the right are filled with 0's.

The result of x << 1 when is x is an 8-bit integer is $26$. So to answer the
previous question: Yes, the size of the integer being shifted matters.
As one last example, let's examine an 8-bit integer x that is again assigned
the value 13. This time, we shift x to the left by 2. This is denoted
x << 2.

We shift each bit over to the left by 2.

Bits that were moved beyond the left boundary are discarded. The blank spaces introduced on the right are filled with 0's.

The result of x << 2 when is x is an 8-bit integer is $52$.
IP addresses
(This section will summarize an extremely well written article on IP addresses provided by the Cisco team.)
An IP address is an address used in order to uniquely identify a device on an IP network. The address is made up of 32 binary bits
Examples of IP addresses include
22.231.113.64194.66.82.1127.0.0.1
The pattern we can observe is four groups of decimal numbers separated by periods. (When we say decimal here, we mean "base 10 number". Basically, not hex, not binary, just plain 0-9 digits. For example, 29 is a decimal number even though it does not contain a decimal point.)
Since computers can only understand binary, IP addresses have to somehow be represented in binary. The standard for representing an IP address (specifically an IPv4 address) in binary is as follows:
- An IP address is represented in the form of 32 binary bits.
- The bits are divided into four groups of 8 individual bits
- This is why IP addresses are composed of four individual numbers.
- Each group of numbers in the IP address will be represented as an octet
- An octet is a grouping of 8 bits
- Since the largest integer that can be represented with 8 bits is 255, no octet in an IP addresses can be larger than 255.
To demonstrate, consider the IP address 99.55.140.82

Note the conversions of the decimal numbers to binary:
- $99_{10} = 1100011_{2}$
- $55_{10} = 110111_{2}$
- $140_{10} = 10001100_{2}$
- $82_{10} = 1010010_{2}$
In the event that a decimal number takes fewer than 8 bits to represent in binary, leading 0s are placed to complete the octet. For example, since $55_{10} = 110111_{2}$, and $110111$ is only 6 digits, the number is represented as $00110111$ when constructing the bits of the IP address.
At this point, we now have 32 bits of 0's and 1's representing an IP address. Even though we divided the 32 bits into four groups of eight when constructing this sequence of bits, that doesn't prevent us from looking at the entire sequence as a whole. Consequently, we can think of an IP address as a plain old integer! So now instead of thinking of the bits as groups, like
01100011 | 00110111 | 10001100 | 01010010
We just smush the bits all together
01100011001101111000110001010010
Then we can convert this binary number to decimal.
$$01100011001101111000110001010010_{2} = 1664584786_{10}$$
So the IP address 99.55.140.82 is equivalent to the integer $1664584786$. We
have just learned how to convert an IP address to an integer. Is it possible to
convert an integer into its associated IP address? Yes!
Integer to IP address
Suppose we've been given the integer $1664584786$ and we need to find the IP address the integer represents.
First, we convert the decimal number to binary. $$1664584786_{10} = 1100011001101111000110001010010_{2}$$
We begin placing this binary number into our 32 bit sequence. We start from the right, so the $0$ at the very gets placed in the last bit and we work our way towards the start.

Since IP addresses must occupy 32 bits, we place leading 0s in the sequence if the binary number has less than 32 bits.

Divide the 32 bits into four octets. Convert each octet to decimal.
- $01100011_{2} = 99_{10}$
- $00110111_{2} = 55_{10}$
- $10001100_{2} = 140_{10}$
- $01010010_{2} = 82_{10}$
Join the decimal values together with periods, with the value of the left-most octet listed first.
99.55.140.82
That's it!
You now know:
- IPv4 IP addresses are represented as 32 bit integers
- How to find the integer value of an IP address
- How to find the IP address of an integer value
Subnetworks and Subnet masks
Subnetworks
A subnetwork (also known as a subnet) is a subdivision of an IP network. A large office network may have a subnet dedicated to accounting, a subnet dedicated to guests, a subnet dedicated to human resources, and so on. Households that receive internet service are connected to large networks managed by their ISP (Internet Service Provider), such as Time Warner and Comcast. When a household sets up a router to enable multiple devices to connect to the internet, they create a tiny subnet within the ISP network.
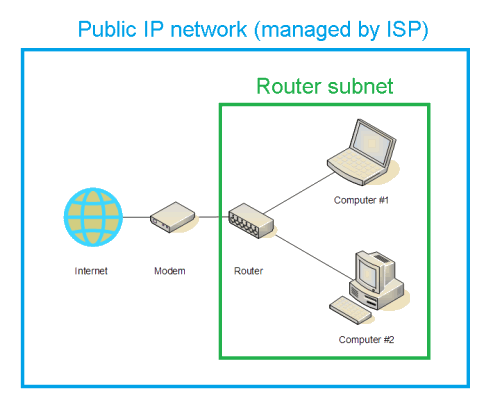
A computer or device connected to a network is called a host of that network. Each host on the network has a unique IP address. If you've ever browsed around your router's web interface, you may have seen a section that lists the devices connected to the router. Each device listed will have a unique IP address.

(Image credit: MyFavoriteGadgets)
If we look closer, we'll see that even though the IP addresses of the router's
hosts are unique, they all start with 192.168.0

This identical prefix for the IP addresses indicates that these hosts are on
this network. However, is it possible for a host with IP 192.168.10.10 to
exist on the network? Does the IP have to start with 192.168.0, or does it
only have to start with 192.168, or maybe even just 192?
We need to learn about network identifiers and subnet masks in order to answer these questions.
Network identifiers
A network identifier, also known as a network prefix, is a portion an IP address that specifies the location of the network itself. Network identifiers are designed so that we can conclude if two hosts reside on the same subnet just by comparing the network identifiers of their IP addresses.
The most recognizable network prefixes are 192.168.0 and 192.168.1. Many
residential routers have one of these two as the default network prefix.

(Image credit: PortForward)
When discussing the internal representation of network prefixes, trailing octets that are omitted are thought of as $0$. So
192.168.0⇒192.168.0.0192.168.1⇒192.168.1.0
Internally, the network identifier is composed of bits at the start of the IP address. (Exactly how many bits make up the identifier is specified by the subnet mask, which we'll discuss soon.) The bits that follow after the network identifier make up the host identifier, which is unique for each device on the network.

(Image credit: TCP/IP Guide)
Since
- subnet masks specify which bits of an IP address are part of the network identifier, and
- subnet masks vary from network to network
it is impossible to split an arbitrary IP address into its network identifier and host identifier components without knowledge of the subnet mask for the network.
As a basic rule of networking, only hosts on the same network can directly communicate. If the network is divided into subnets, then only hosts on the same subnet can directly communicate, even if the two hosts are within the same network.
Let's recap some of information we've discussed regarding IP addresses:
- Every host has an IP address
- Every IP address begins with a network identifier
- Hosts on the same subnet will have the same network identifier
- Hosts not on the same subnet will have different network identifiers
- Only hosts on the same subnet can directly communicate
From this information, we can conclude that two hosts should not be allowed to directly communicate unless their IP addresses begin with the same network identifier. This is because by definition the network identifier specifies what network the host is on, and if two hosts have different network identifiers they must be on different networks.
Example: Consider the IP addresses of two hosts: 192.168.1.1 and
192.168.2.1. If the network identifier for 192.168.1.1 was 192.168.1.0,
then the host with address 192.168.2.1 would not be able to communicate with
the host at 192.168.1.1 since 192.168.1.0 is not equal to 192.168.2.0.

NOTE: Two hosts residing on different networks can still communicate through routers, they just can't communicate directly
But notice in the router menu listed above there is no "network prefix" or "network identifier" option. This is because the subnet mask defines how to extract the network identifier from the IP addresses of hosts on the subnet.
Subnet masks
A subnet mask is a sequence of 32 bits defined during network configuration that specifies what significant bits (left-most bits) of an IP address serve as the network identifier. Subnet masks help answer the question "What is the network identifier for this IP address according to the network's rules?" Remember
- all hosts on the same subnet must begin with the same network identifier
- only hosts on the same subnet can directly communicate
so having a way to extract and compare the network identifiers from two IP addresses is vital in determining if the hosts are allowed to directly communicate. Subnet masks power this extraction and comparison process.
The most recognizable subnet mask is 255.255.255.0. It's the default subnet mask
used by most residential routers.
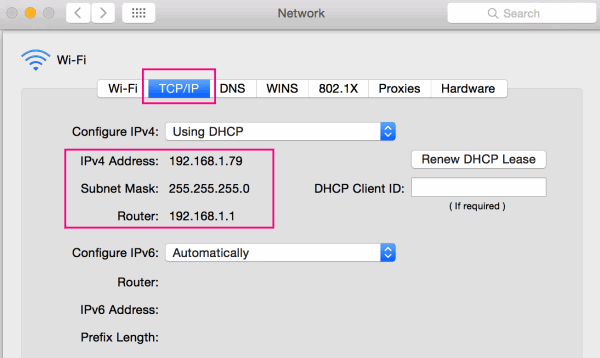
(Image credit: Kecodoc)
Here is the binary representation of the subnet mask 255.255.255.0

How exactly does a subnet mask help determine the network identifier of an IP address? Through the bitwise AND operation discussed earlier in the article. Let's look at an example.
Suppose we are configuring a basic residential router. We have decided the
network identifier will be 192.168.1.0, meaning valid host IP addresses would
look like
192.168.1.5192.168.1.12192.168.1.253
Specifying a subnet mask of 255.255.255.0 will accomplish this. How so? Let's
line up the subnet mask with the binary representation of the IP address
192.168.1.5. By performing a bitwise AND of the two sequence of bits, we will
reveal the desired network identifier of 192.168.1.0.
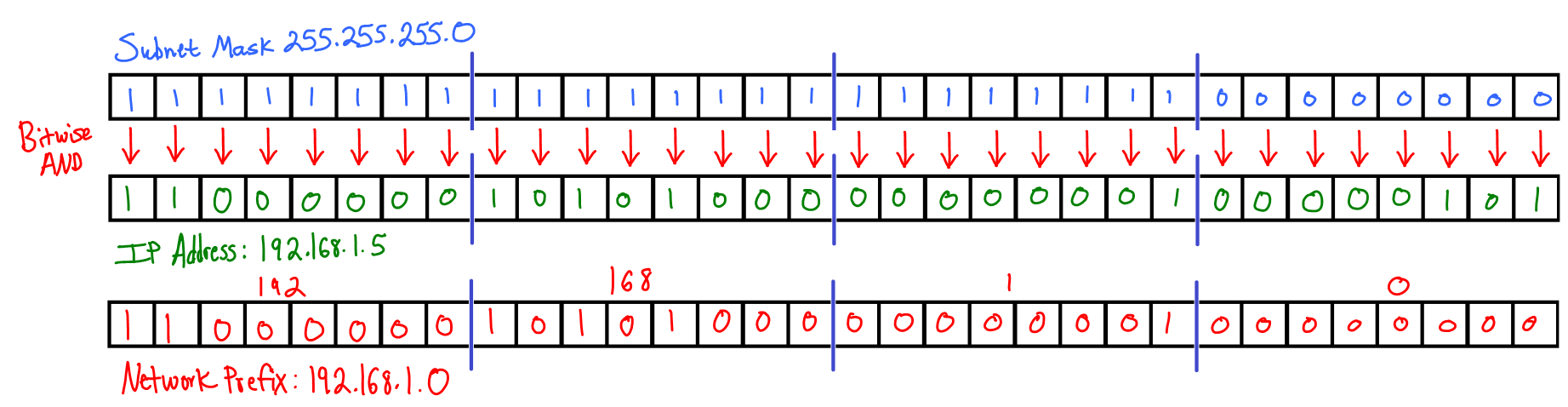
We see that the subnet mask 255.255.255.0 ANDed with the IP address
192.168.1.5 did in fact extract the correct network identifier, 192.168.1.0.
But how did we know to choose that specific subnet mask?
The most common octet groupings within a subnet mask are $255$, and $0$. This is because $$255_{10} = 11111111_{2}$$ and $$0_{10} = 000000_{2}$$ Why are these values significant? Let's observe what happens when we perform a bitwise AND between the octet 255 and any other octet.

255 & 142 == 142

255 & 68 == 68

255 & 77 == 77
The result of ANDing $255$ and any other octet results is just the other octet. What about if we AND $0$ with any other octet?

0 & 142 == 0

0 & 68 == 0

0 & 77 == 0
The result of ANDing $0$ and any other octet results is just $0$.
We can use this behavior to our advantage. If we want the network identifier to occupy the first three octets of an IP address, then we just have to set the first three octets of the subnet mask to $255$ with the last octet set to 0. If we want the network identifier to occupy only the first two octets of an IP address, then we have to set the first two octets of the subnet mask to $255$ with the last two octets to 0.
Let's revisit a previous example with this information in mind.
In the example, we stated the identifier for a preconfigured network was
192.168.1 (which gets expanded to 192.168.1.0). Consequently, we need to
extract the first 3 octets of a host's IP address and compare the result against
192.168.1.0 to determine if the host is on the subnet. From what we just
discussed above, if we want a subnet mask that helps us extract the first three
octets from a host's IP address, the first three octets of the subnet mask
should be 255 and the last octet should be 0. Thus the subnet mask comes out to
255.255.255.0. Does this subnet mask get the job done? Let's see.

We see that the network prefix extracted from the address 192.168.1.5 is
192.168.1.0, which matches the identifier for the network. This lets us
conclude that the host with IP 192.168.1.5 is part of the subnet. That's how
subnets are used!
Notice how the subnet masks we've used have all been a sequence of bits
starting with a bunch of $1$'s followed by a bunch of $0$'s that fill up the
left over bits. Instead of going through the trouble of defining the octets for
the subnet masks, it would be easier to just say "I want a subnet mask that
starts with this many $1$'s". For example, instead of saying "the IP address
192.168.1.5 with subnet mask 255.255.255.0", what if we could instead say
"the IP address 192.168.1.5 with a subnet mask starting with 24 $0$'s".
This shorthand is exactly what CIDR provides.
CIDR (Classless Inter-Domain Routing)
(Information provided by Wikipedia).
While it is technically possible to have a subnet mask whose bit sequence contains some zeros within the sequence of $1$'s, such practice is rarely used. An overwhelming majority of subnet masks have bits sequences that begin with only $1$'s and once the first $0$ is encountered, the rest of the bits will be $0$.
An example of a weird, but legal, subnet mask

An example of a standard, cookie-cutter subnet mask

Since the most common scenario is to have a subnet mask that begins with contiguous $1$'s and ends with contiguous $0$'s, all that's really required is for us to specify how many $1$'s the subnet mask should begin with. Since IPv4 addresses are 32 bits, the number of trailing $0$'s is just $32$ minus the number of leading $1$'s specified.
Equivalence with subnet masks
CIDR notation provides a way to express this idea. The notation 192.168.2.1/24
means "The IP address 192.168.2.1 with the subnet mask resulting from $24$
leading $1$'s". For CIDR notation, I've seen the number after the slash referred
to as the CIDR number, or the netmask.
Remember, the goal of the subnet mask is to help us calculate the network identifier from a given IP address on the network. The goal of CIDR notation is to provide a concise and flexible way to specify the subnet mask. Thus CIDR notation still allows us to extract the network identifier from the IP address.
What is the network identifier for 192.168.2.1/24?

So $/24$ is equivalent to the subnet mask of 255.255.255.0. Now that we have
an IP address and a subnet mask, we can bitwise AND the IP address and subnet
mask together as described earlier in the article. The resulting network
identifier for this example is 192.168.2.0 - make sure you work this out on
your own and verify this for yourself!
Assessment
Complete the following exercise problems to verify your understanding of the discussed material.
Problem 1
Create a program that, given an IP address and its accompanying subnet mask, outputs the network identifier and host identifier.
Problem 2
Create a program that, given the IP address / Subnet mask pairs of two hosts, determines if the hosts can possibly be on the same network.
Problem 3
Create a program that converts an IPv4 address octets into its equivalent integer form.
Problem 4
Create a program that validates if a string is a valid IPv4 address in CIDR notation.
Problem 5
Create a program that converts an integer representing an IPv4 address into its octet form. Additionally, use ASCII art to print out the individual bits if the IP address in sections of 8 like the examples in this article.
Problem 6
The integer value of the IP address 99.55.140.82 is 1664584786. Given only
the number 1664584786, how could you extract and display the value of the
first octet (99) without using any string based operations? Can you use a
similar process to display the value of the 2nd, 3rd, and last octets?
Conclusion
You have learned what exactly composes an IP address. You can also determine if two machines are on the same network by analyzing their IP addresses and the accompanying subnet masks. You have learned about the CIDR notation and CIDR number's equivalence with a subnet mask.